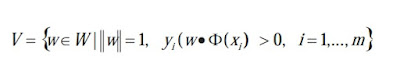PROLOGUE.
With the growing need for multimedia information retrieval from the Web, such as picture and video retrieval, it's becoming more difficult to train a classifier when the training dataset contains a small number of labelled data and a big number of unlabeled data.
Traditional supervised and unsupervised learning approaches are ineffective in solving such issues, especially when the data is in a high-dimensional environment.
Many strategies have been presented in recent years that may be essentially split into two categories: semi-supervised and active learning (AL).
Since the turn of the century, a number of academics have introduced Active Learning with SVM (ALSVM) methods, which have been regarded as an efficient technique for dealing with high-dimensionality issues.
We discuss the state-of-the-art of ALSVM for tackling classification issues in this work, given their fast progress.
CONTEXT.
The overall structure of AL is shown below.
It is evident that the learner may enhance the classifier by actively picking the "optimal" data from the possible query set Q and adding it to the current labeled training set L after receiving its label throughout the procedures.
AL's most important feature is its sample selection criteria.
AL was formerly mostly utilized in conjunction with the neural network algorithm and other learning algorithms.
The sample minimizing either variance (D. A. Cohn, Ghahramani, & Jordan, 1996), bias (D. A. Cohn, 1997), or generalization error (Roy & McCallum, 2001) is queried to the oracle in statistical AL.
Although these approaches have a solid theoretical basis, they are limited in their application due to two frequent issues: how to estimate the posterior distribution of the data and the excessively high computational cost.
To address the aforementioned two issues, a number of version space-based AL methods have been proposed, which are based on the assumption that the target function can be perfectly expressed by one hypothesis in the version space and that the sample that can reduce the volume of the version space is chosen.
Query by committee (Freund, Seung, Shamir, & Tishby, 1997) and SG AL are two examples (D. Cohn, Atlas, & Ladner, 1994).
However, before the advent of version space-based ALSVMs, they were intractable due to the complexity of version space.
Researchers have combined AL with SVM to cope with semi-supervised learning issues, such as distance-based (Tong & Koller, 2001), RETIN (Gosselin & Cord, 2004), and Multi-view (Cheng & Wang, 2007) based ALSVMs, thanks to the popularity of SVM in the 1990s.
VERSION SPACE BASED ACTIVE LEARNING WITH SVM
Almost all extant heuristic ALSVMs aim to discover the sample that can minimize the size of the version space, either explicitly or indirectly.
In this part, we'll go through their theoretical underpinning before going over several common ALSVMs.
Existing well-known ALSVMs are discussed in the context of version space theory, followed by a short description of certain mixed techniques.
Finally, we'll talk about ALSVM research trends and draw conclusions for the study.
Theory of Version Space.
Based on the Approximation of Probability Machine learning's purpose is to create a consistent classifier with the lowest generalization error constraint.
The Gibbs generalization error bound (McAllester, 1998) is defined as follows:
where PH is a prior distribution over hypothesis space H, V(z) is the version space of the training set z, m is the number of z, and d is a constant in the range [0, 1].
If the distribution of the version space is uniform, the volume of the version space controls the generalization error limits of the consistent classifiers.
This gives a theoretical foundation for ALSVMs based on version space.
With SVM, query by committee.
(Freund et al., 1997) developed a technique in which 2k classifiers were randomly picked, and the sample on which these classifiers have the most disagreement may roughly half the version space, and then the oracle was queried.
The intricacy of the structure of the version space, on the other hand, makes random sampling within it challenging.
(Warmuth, Ratsch, Mathieson, Liao, & Lemmem, 2003) successfully used a billiards approach to randomly choose classifiers in the SVM version space, and testing revealed that its performance was equivalent to that of the standard distance-based ALSVM (SD-ALSVM), which will be discussed later.
The flaw is that the procedures take a long time to complete.
Standard Active Learning with SVM over a Long Distance.
The version space for SVM is defined as follows:
where Φ(.) denotes the function which map the original input space X into a high-dimensional space Φ X )( , and W denotes the parameter space. SVM has two properties which lead to its tractability with AL.
The first is its duality property that each point w in V corresponds to one hyperplane in Φ X )( which divides Φ X )( into two parts and vice versa.
The other property is that the solution of SVM w* is the center of the version space when the version space is symmetric or near to its center when it is asymmetric.
(Tong & Koller, 2001) deduced a lemma from the above two properties: the sample closest to the decision boundary may reduce the predicted size of the version space the quickest.
As a result, the oracle will be requested for the sample closest to the decision border shown in the Figure below:
This is the SD-ALSVM, which has minimal extra calculations for picking the query sample and excellent performance in real-world applications.
Distance Based Active Learning with SVM in Batch Running Mode
(Tong & Koller, 2001) used batch query to choose several samples that are closest to the decision boundary.
However, as shown in figure below, adding a batch of such samples does not guarantee t
he maximum decrease in the size of version space.
Although each sample can almost half the version space, three samples combined can only lower the version space by around 1/2, less than 7/8.
This was attributed to the tiny angles between their induced hyperplanes, as can be shown.
(Brinker, 2003) developed a novel selection technique that incorporates a diversity measure that examines the angles between the induced hyperplanes to solve this issue.
In the present round, if the labeled set is L and the pool query set is Q, then the further added sample xq should be independent on the frontier and an adaptive approach was devised to adjust s throughout the feedback rounds based on the diversity requirement.
Where yxkyxh)() denotes the number of relevant and irrelevant samples in the queried set in the ith iteration, and rrel(i) and rirrl(i) signify the number of relevant and irrelevant samples in the queried set in the ith iteration.
The amount of relevant and irrelevant samples in the searched set will be about equal as a result of this method.
The Mean Version Space Criterion.
(He, Li, Zhang, Tong, & Zhang, 2004) suggested a selection criteria based on reducing the mean version space, which is described as
where )(( ki xVVol + ( )(( ki xVVol − ) denotes the volume of the version space after adding an unlabelled sample xk into the ith round training set.
The volume of the version space as well as the posterior probability are included in the mean version space.
As a result, they concluded that the criteria is superior than the SD-ALSVM.
However, this method's calculation takes a long time.
Active Learning with Multiple Views.
Multi-view approaches, in contrast to algorithms that are based on a single feature set, are based on numerous sub-feature sets.
Several classifiers are trained on various sub-feature sets initially.
The contention set, from which questioned examples are chosen, is made up of the samples on which the classifiers have the most disagreements.
First, it was used in AL (I. Muslea, Minton, & Knoblock, 2000), and then it was combined with ALSVM (Cheng & Wang, 2007) to generate a CoSVM algorithm that outperformed the SD-ALSVM.
Because they see the data from diverse perspectives, several classifiers may detect the unusual examples.
This attribute is quite beneficial for locating components that belong to the same category.
Multi-view based approaches, on the other hand, need that the relevant classifier be able to correctly categorize the samples and that all feature sets be uncorrelated.
In real-world applications, ensuring this requirement is tough.
MIXED ACTIVE LEARNING.
In this part, instead of single AL techniques as in the previous sections, we'll talk about two mixed AL modes: one that combines diverse selection criteria, and the other that incorporates semi-supervised learning into AL.
Hybrid Active Learning.
Rather than creating a new AL algorithm that works in all scenarios, some academics think that integrating several approaches, which are generally complimentary, is a superior approach since each method has its own set of benefits and drawbacks.
The parallel mode structure of the hybrid approach is obvious.
The important thing to remember here is how to adjust the weights of various AL techniques.
Most previous methods employed the simplest method of setting fixed weights based on experience.
Most Relevant/Irrelevant (L. Zhang, Lin, & Zhang, 2001) techniques may assist to stabilize the decision border, but they have poor learning rates; traditional distance-based approaches have high learning rates, but their frontiers are unstable at the early feedbacks.
Taking this into account, (Xu, Xu, Yu, & Tresp, 2003) combined these two tactics to get greater results than if they had used just one.
As previously mentioned, diversity and distance-based techniques are complimentary, and (Brinker, 2003), (Ferecatu, Crucianu, & Boujemaa, 2004), and (Dagli, Rajaram, & Huang, 2006), respectively, coupled angle, inner product, and entropy diversity strategies with conventional distance-based strategies.
However, the fixed weights technique does not work well with all datasets or learning iterations.
As a result, the weights should be adjusted dynamically.
All the weights were started with the same value in (Baram, El-Yaniv, & Luz, 2004), and were adjusted in subsequent iterations using the EXP4 method.
As a consequence, the resultant AL algorithm is routinely demonstrated to perform almost as good as, and occasionally even better than, the best algorithm in the ensemble.
Semi-Supervised Active Learning.
1. Active Learning with Transductive SVM (Semi-Supervised Active Learning)
A few labeled data in the early stages of SD-ALSVM may cause a significant departure of the current solution from the genuine solution; however, if unlabeled samples are taken into account, the solution may be closer to the true solution.
(Wang, Chan, & Zhang, 2003) shown that the smaller the version space is, the closer the present answer is to the genuine one.
To create more accurate intermediate solutions, they used Transductive SVM (TSVM).
However, some research (T. Zhang & Oles, 2000) questioned whether TSVM is as useful in principle as it is in reality when dealing with unlabeled data.
Instead, (Hoi & Lyu, 2005) used semi-supervised learning approaches based on Gaussian fields and Harmonic functions, with considerable gains observed.
2. Incorporating EM into Active Learning is the second step.
Expectation Maximization (EM) was integrated with the approach of querying by committee (McCallum & Nigam, 1998).
And (Ion Muslea, Minton, & Knoblock, 2002) combined the Multi-view AL method with EM to create the Co-EMT algorithm, which may be used when the views are incompatible and correlated.
PROJECTIONS FOR THE FUTURE.
How to Begin the Active Learning Process.
Because AL may be thought of as the issue of finding a target function in version space, a solid starting classifier is crucial.
When the objective category is large, the initial classifier becomes more significant since a defective one might lead to convergence to a local optimum solution, which means that certain areas of the objective category may not be accurately covered by the final classifier.
Long-term learning (Yin, Bhanu, Chang, & Dong, 2005), and pre-cluster (Engelbrecht & BRITS, 2002) techniques are all promising.
Feature-Based Active Learning
In AL, the oracle's comments may also aid in identifying essential characteristics, and (Raghavan, Madani, & Jones, 2006) shown that such efforts can greatly increase the final classifier's performance.
Principal Components Analysis was used to discover essential aspects in (Su, Li, & Zhang, 2001).
There are few reports on the subject that we are aware of.
Active Learning Scaling
The scalability of AL to extremely big databases has not yet been thoroughly investigated.
However, it is a significant problem in a number of real-world applications.
Some ways to indexing databases (Lai, Goh, & Chang, 2004) and overcoming the concept complications associated with the dataset's scalability have been offered (Panda, Goh, & Chang, 2006).
INFERENCE
In this study, we review the ALSVM approaches, which have been the subject of intensive research since 2000.
Within the context of the notion of version space minimization, we initially concentrate on descriptions of heuristic ALSVM techniques.
Then, to balance the shortcomings of single approaches, mixed methods are proposed, and lastly, future research trends concentrate on strategies for choosing the initial labeled training set, feature-based AL, and AL scaling to extremely large databases.
GLOSSARY OF TERMS USED:
Heuristic Active Learning is a class of active learning algorithms in which the sample selection criteria are determined by a heuristic objective function. Version space based active learning, for example, selects a sample that reduces the size of the version space.
Hypothesis Space: The collection of all hypotheses in which the objective hypothesis is expected to be found is known as Hypothesis Space.
Semi-Supervised Learning: A type of learning methods in which the classifier is trained using both labelled and unlabelled data from the training dataset.
Statistical Active Learning: A class of active learning algorithms in which the sample selection criteria are based on statistical objective functions such minimization of generalization error, bias, and variance. In most cases, statistical active learning is statistically optimum.
Supervised Learning: The collection of learning algorithms in which all of the samples in the training dataset are labeled is known as supervised learning.
Unsupervised Learning is a class of learning algorithms in which the training dataset samples are entirely unlabeled.
Version Space: The subset of the hypothesis space that is compatible with the training set is known as version space.
Find Jai on Twitter | LinkedIn | Instagram
You may also want to read more about Artificial Intelligence here.